1365. Dijkstra Algorithm
You are given a directed weighted graph. Find the shortest distance from
vertex s to vertex f.
Input. The
first line contains three integers n, s, and f (1 ≤ n
≤ 100, 1 ≤ s, f ≤ n), where n is the
number of vertices in the graph. Each of the following n lines contains n
integers, representing the adjacency matrix of the graph. The integer at
the i-th row and j-th column indicates the weight of the
edge from vertex i to vertex j. A value of -1 means there is no
edge between the vertices, while a non-negative value represents the weight of
the edge. The main diagonal of the matrix always contains zeros.
Output. Print the shortest
distance from vertex s to vertex f. If there is no
path between the two vertices, print -1.
|
Sample
input |
Sample
output |
|
3 1 2 0 -1 2 3 0 -1 -1 4 0 |
6 |
SOLUTION
graphs
– Dijkstra algorithm
Algorithm analysis
Example
The graph given in the example looks like this:
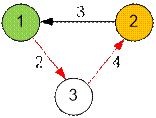
The shortest distance from vertex 1 to vertex 2 is 2 + 4 = 6.
Algorithm implementation
Let’s declare the
constants and arrays we’ll use.
#define MAX 110
#define INF
0x3F3F3F3F
int m[MAX][MAX], used[MAX], d[MAX];
Read the input data.
scanf("%d %d %d",
&n, &s, &f);
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
{
scanf("%d",
&m[i][j]);
if
(m[i][j] == -1) m[i][j] = INF;
}
Initialize the arrays.
memset(used, 0, sizeof(used));
memset(d, 0x3F, sizeof(d));
d[s] = 0;
Start the loop for Dijkstra’s algorithm. Since the graph
contains n vertices, n – 1 iterations will be sufficient.
for (i = 1; i < n; i++)
{
Find the vertex with the smallest value of d[j] among
those for which the shortest distance from the source is not calculated (i.e.,
for which used[j] = 0). Let this vertex be w.
mind = INF;
for (j = 1; j <= n; j++)
if (used[j] == 0 && d[j] <
mind) { mind = d[j]; w = j; }
If it is impossible to find a vertex to include in the set of
vertices for which the shortest distance is already calculated, terminate the
algorithm.
if (mind == INF) break;
Relax all the edges outgoing from vertex w.
for (j = 1; j <= n; j++)
if (used[j] == 0) d[j] = min(d[j], d[w]
+ m[w][j]);
Mark that the shortest distance to w is calculated (it
is stored in d[w]).
used[w] = 1;
}
Print the answer – the value of d[f]. If it is equal
to infinity, then there is no path to vertex f.
if (d[f] == INF) d[f] = -1;
printf("%d\n", d[f]);
Python implementation
Let’s declare the constants we’ll use.
MAX = 110
INF = float('inf') / 2
Read the input data.
n, s, f = map(int, input().split())
m = [[0] * (n + 1)]
for _ in range(n):
row = list(map(int, input().split()))
m.append([0] + [INF if x == -1 else x for x in row])
Initialize the lists.
used = [False] * (n + 1)
d = [INF] * (n + 1)
d[s] = 0
Start the loop for Dijkstra’s
algorithm. Since the graph contains n vertices, n – 1 iterations
will be sufficient.
for _ in range(n - 1):
Find the vertex with the smallest
value of d[j] among those for which the shortest distance from the
source is not calculated (i.e., for which used[j] = 0). Let this vertex
be w.
mind = INF
w
= -1
for j in range(1, n + 1):
if not used[j] and d[j] < mind:
mind = d[j]
w = j
If it is impossible to find a vertex
to include in the set of vertices for which the shortest distance is already
calculated, terminate the algorithm.
if mind == INF:
break
Relax all the edges outgoing from
vertex w.
for
j in range(1, n + 1):
if not used[j]:
d[j] = min(d[j], d[w] + m[w][j])
Mark that the shortest distance to w
is calculated (it is stored in d[w]).
used[w] = True
Print the answer – the value of d[f].
If it is equal to infinity, then there is no path to vertex f.
print(-1 if d[f] == INF else d[f])
